原子膜とかけて熱帯魚と解く。そのココロは…? -ナノ物理学と生物学を繋ぐチューリング・パターンの新理論-
電気通信大学の伏屋 雄紀准教授と北海道大学の勝野 弘康研究員およびPSL研究大学・Kamran Behnia教授、スタンフォード大学・Aharon Kapitulnik教授からなる国際共同研究チームは、原子間に働く三種類の力を取り入れた新しい理論模型を構築することで、ビスマス単原子膜(原子1個分の厚み)に現れるナノスケールの奇妙な模様が、熱帯魚の模様など生物のパターン形成と同じ「チューリング・パターン※1」であることを明らかにしました。
これまで生物学や化学分野で見られたチューリング・パターンは数cmから0.1mm程度がほとんどでした。今回の研究により、従来のものより圧倒的に小さい1nm(10億分の1m)幅の極微小なチューリング・パターンが見つかった上、その発生メカニズムまで明らかになりました。これにより、生物学、化学からナノ物理学までがチューリング理論により繋がったことになります。
国際チームはさらに、ビスマス単原子膜のように硬い結晶が、生物と同じように自分で勝手にキズを治してしまうことを発見しました。このメカニズムを応用すれば、従来とは全く異なる非線形な反応拡散方程式※2を用いて、完璧に平坦な超薄膜や新しい量子デバイスを作製できる可能性があり、学術分野のみならず、ナノエレクトロニクス分野への貢献が期待されます。
本研究成果は、“Nature Physics”に2021年7月9日掲載されました。また、英国王立化学会誌“Chemistry World”に2021年7月14日紹介されました。

熱帯魚とビスマスの繋がりを発見
■研究成果のポイント
・ビスマスの原子膜に現れる奇妙な模様が、生物の模様と同じ「チューリング・パターン」であることを解明。
・固体の表面にキズがついても、生物のように自己修復する性質があることを発見。
・非線形偏微分方程式を用いた新しいナノスケールデバイスの作製法に繋がると期待。
■研究の背景
<いかにして生物の模様が作られるか>
熱帯魚の縞模様など、生物の模様はどのようにして作られているのでしょうか?この問題に画期的な答えを見出したのが、数学者のアラン・チューリングです。チューリングは、旧ドイツ軍の暗号“エニグマ”を解読したことや、現在の計算機の元を発案したことで知られており、ちょうど今年の6月23日から新しい50ポンド紙幣に描かれています。1952年にチューリングは簡単な数式から生物の模様に似たパターンを生み出す、驚くべき理論を発表しました。そうしてできる模様は「チューリング・パターン」とよばれ、その後の研究で熱帯魚やヒョウ柄など、様々な生物の模様を説明することに成功しています。生物学にとどまらず、1990年代には化学の分野でも亜塩素酸-ヨウ化物-マロン酸(CIMA)溶液においてチューリング・パターンが実際に確認されました。
<模様の大きさは変えられる?>
これまでに確認されているチューリング・パターンのほとんどは、10cm~0.1mm程度の範囲に限られています。しかしチューリングの理論にはパターンの大きさを制限する要素は入っていません。ということは、発見されていないだけで、パターンはどこまでも小さくなるのでしょうか?あるいは、チューリング理論で捉え切れていない未知の要素が存在し、それによりパターンの大きさは制限されているのでしょうか?
今回の研究により、この問いに新たな答えを与えることができました。硬い素材でしかも1nm(10億分の1メートル)という極微小のチューリング・パターンが実存することを、理論的にも実験的にも、明確に確認することができたのです。このことは、あらゆる大きさのチューリング・パターンが存在している可能性をも示唆しています。
<偶然の発見>
奇妙な模様がビスマス単原子膜で見つかったのは、全くの偶然でした。近年、固体物理学の分野では「トポロジカル物質※3」が大変熱心に研究されています。今回の研究チームの一員であるKapitulnik教授(スタンフォード大)の実験グループは、トポロジカル物質科学の観点から注目されていた、ビスマス単原子膜の作製に2017年に成功しました。しかし、ビスマス単原子膜の構造を原子レベルで詳しく観察すると、これまで見たこともない奇妙な縞模様ができていたことに気づきました(図1b左)。縞と縞の間隔はわずか1nm。極微の世界の模様でした。その様な模様はこれまで観測されたことがなく、どうして模様が現れるのか、その理由は全く分かりませんでした。
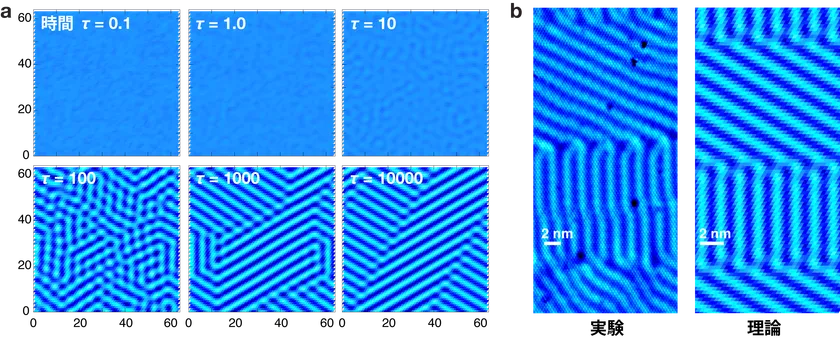
図1 (a) ビスマス単原子膜で時間と共にチューリング・パターンが形成される様子。(b) 実験と理論の比較。
■研究の内容
<アイデアは得たものの>
Kapitulnik教授からビスマスの模様を見せられた伏屋准教授は、一目見て「チューリング・パターンではないか?」という奇抜な発想を得ました。しかし、チューリング・パターンは主に数理生物学で研究されているもので、原子スケールを扱う固体物理学とはあまりにもかけ離れています。過去に類似した研究は一例もなく、アイデアを持ったものの、それをどう証明すればよいかの手がかりは全くありませんでした。
原子間に働く力は非常に複雑で、それら全てを考えるのは容易ではありません。特に重要と思われる要素だけに絞ってもその組合せを全て試すのに大変な労力を必要とします。3年間の試行錯誤を経て、ビスマス同士の原子間力と、基板のセレン原子とビスマス間の力に加え、共有結合に由来する三体相互作用までを考慮することで、実験と酷似するパターンが得られることを突き止めました(図1)。さらに理論を推し進め、このパターンがチューリング・パターンであることを、解析計算(手計算)によって証明することにも成功しました。
<キズを勝手に治す固体の発見>
チューリング・パターンは、非平衡状態で波が干渉して生成されています。パターンは一見静的ですが、実は動的です。この動的な性質をより明確に捉えるため、チームは生成されたパターンにわざと“キズ”をつけてシミュレーションしてみました。すると、まるで原子に意識があるかのように、キズはみるみる元通りに修復されることが分かりました(図2)。当初はキズが修復されたとしても、元と異なる方向の縞模様が現れ、何らかの傷跡が残ると予想していました。しかし実際は、縞領域境界の構造まで“完全治癒”されることが分かりました。

図2 原子膜につけた円形のキズが勝手に修復される。
■研究の意義
<非平衡熱力学の新しい展開へ>
チューリング・パターンは、熱平衡状態から遠く離れた非平衡状態で現れる散逸構造※4(プリゴジン、1977年ノーベル化学賞)の一つとして長年研究されてきました。これまで散逸構造は主に目で見える巨視的な現象として扱われてきましたが、今回の研究によって、原子スケールでも現れることが分かりました。これにより、微視的スケールから非平衡熱力学を研究する新たな道が拓けました。また、従来の色素や溶液などソフトマターではなく、“硬い”固体でパターンが現れたことから、固体物理学が得意とする実験手法が使えるようになりました。このことで、散逸構造の研究の幅がより拡がると期待されます。
<新しいメカニズムで新しいデバイスをデザインする>
ナノエレクトロニクスでは、凹凸(模様)のない完全に平坦な超薄膜を作る必要があります。これまで研究者は、凹凸が現れない条件を、経験と勘で探り当ててきました。今回発見された原理を応用すれば、経験や勘に頼ることなく、効率的に凹凸のない完璧な超薄膜を作れる可能性があります。一方、条件を変えれば異なるパターンも創り出せることが分かりました。この技術を応用すれば、新しいメカニズムで、従来の平衡熱力学では予測できなかった、新しいナノデバイスをデザインできることにも繋がります。
タイトル : Nanoscale Turing patterns in a bismuth monolayer
著者 : Yuki Fuseya, Hiroyasu Katsuno, Kamran Behnia,
and Aharon Kapitulnik
掲載誌 : Nature Physics
公開日 : 2021年7月9日
本誌リンク: https://www.nature.com/articles/s41567-021-01288-y
DOI : 10.1038/s41567-021-01288-y
<紹介記事>
タイトル : Tiniest Turing patterns found in atomically thin bismuth
著者 : Philip Ball
掲載誌 : Chemistry World(英国王立化学会誌)
公開日 : 2021年7月14日
■用語解説
※1 チューリング・パターン
コーヒーにミルクを注ぐと次第に均一なカフェオレができるように、常識的には、拡散することで状態は均一になる。しかし数学者のアラン・チューリングは、時間的・空間的に不均一な状態が拡散によって誘起されることを、「形態形成の化学的基礎」(1952)と題した論文中で示した。そうしてできる模様をチューリング・パターンとよぶ。
※2 反応拡散方程式
化学反応における各種化学物質の濃度と時間変化を、それらの拡散も含めて記述する連立偏微分方程式。化学反応だけでなく、物理学、生物学に現れる非線形現象を広範囲に記述することができる。上記チューリングの論文(1952)中に現れる方程式も、本質的に反応拡散方程式である。
※3 トポロジカル物質
トポロジー(位相幾何)とは、対象の形を連続的に変えても(切ったり貼り付けたりはしない)幾何学的特徴が保たれる性質に注目した数学の分野である。ドーナツとコーヒーカップは穴が1つという点で同じトポロジーだが、穴のあいていないボールとはトポロジーが異なる。トポロジカル物質とは、物質の量子的な性質(波動関数)のトポロジーが、従来物質と異なる物質を指す。
※4 散逸構造
エネルギーなどの散逸があり、物質系が熱平衡から十分離れた非平衡状態にあるとき、巨視的な構造が現れる場合がある。これを散逸構造とよぶ。イリヤ・プリゴジンが提唱し、その業績からノーベル化学賞(1977)を受賞した。熱い味噌汁をしばらく放っておくと、対流によりパターンが生じる。これも散逸構造の一つである。チューリングの理論は主に形態形成との関係についてのみ議論されてきたが、プリゴジンはこれをより広い視点から、散逸現象の一つであることを明らかにした。